Atividades
Práticas
Aula
Prática 1
Conversão entre Bits, Bytes, Megabytes, Gigabytes e Terabytes
Você pode testar seus conhecimentos acerca desse tipo de conversão executando os exercícios disponíveis no segundo capítulo do PLT, localizados na página 37 sob número 7, transcritos abaixo.
Exercício
7) Indique o valor de x nas seguintes expressões
a)
65.536 = xK
b)
12.288K = xM
c)
19.922.944 = xM
d)
8 Gbytes = x bytes
e)
64 Kbytes = x bits
f)
262.144 bits = xK bits
g)
16.777.216 palavras = x palavras (usando a menor unidade
possível, no caso M – mega)
h)
128 Gbits = x bits
i)
512 K células = x células
j)
256 Kbytes = x bits
Para conferi-los, você pode recorrer à seguinte ferramenta
Conversão de Bases Você tem
dúvidas? Consulte o
resumo Sistema de Conversão
Numérica Tente fazer
alguns dos seguintes exercícios do PLT Página 60 Exercício 13 e) (5331)8 = ( )2
13) c)
(11011100011)2 = ( )16 13) d) (2BEF5)16 = ( )8 Decimal
para Octal Página 59 –Exercício 6) a) 917 Octal
para Decimal Página 59 –Exercício 7) a) 405 Decimal
para Hexadecimal Página 59 – Exercício 10) a) 2136 Hexadecimal
para Decimal Página 59)
Exercício Confira sua
solução usando a ferramenta de conversão disponível em http://faculty.mc3.edu/ Para usá-la,
observe a seguinte legenda, contendo a tradução da língua inglesa para a língua
portuguesa: Conversion
between bases – Conversão entre bases Convert –
Converter Clear –
Limpar Binary –
Binário O uso da
ferramenta é simples: 1) Selecione a base em que está
expresso o número que você quer converter (Binary
para binário, Octal para octal
e Hexadecimal (base 16) para hexadecimal). Digite esse número na caixa Base X.
Caso o número esteja em base decimal, digite o número na caixa Base 10. 2) Se o número estiver expresso em base
diferente de 10 (decimal), clique em Convert ao lado da caixa Base X e o número será convertido
para base decimal. Caso esse seja o seu objetivo, pode interromper a conversão
neste momento. Observe que será apresentada uma janela na qual são explicadas
as contas feitas para realizar a conversão. Por exemplo, para converter 100001
da base 2 para a base 10, será exibida a seguinte
explicação: To convert
100001 from base 2 to decimal (base 10), multiply the digits
by powers of the base. Start with
the rightmost digit and multiply by 2 to the 0th power (which is 1.) Then multiply the next digit by 2 to the 1st
power and so on. Add up all the
products. 1 x 2 raised
to the power 0 (1)=1 0 x 2 raised
to the power 1 (2)=0 0 x 2 raised
to the power 2 (4)=0 0 x 2 raised
to the power 3 (8)=0 0 x 2 raised
to the power 4 (16)=0 1 x 2 raised
to the power 5 (32)=32 the resulting
sum = 33 Essa explicação pode ser traduzida da seguinte maneira: Para converter 100001 da base 2
para decimal (base 10), multiplique os dígitos pelas potências da base. Comece com o dígito mais a direita e multiplique por 2 elevado a 0 (que vale 1). Então multiplique o próximo dígito
por 2 elevado a primeira e assim por diante. Some os
resultados de todos esses produtos. 1 x 2 elevado à potência 0 (1)=1 0 x 2 elevado à potência 1 (2)=0 0 x 2 elevado à potência 2 (4)=0 0 x 2 elevado à potência 3 (8)=0 0 x 2 elevado à potência 4 (16)=0 1 x 2 elevado à potência 5 (32)=32 A soma resultante vale 33. 3) Se o número estiver expresso em base 10
(decimal), vá para o passo seguinte. 4) Selecione a base para a qual você
deseja converter o número (Binary para binário, Octal para octal e Hexadecimal (base
16) para hexadecimal) e clique em Convert ao lado da
caixa Base 10. O resultado será apresentado ao lado da caixa Base X. 5) Observe que será apresentada uma
janela na qual são explicadas as contas feitas para realizar a conversão. Por
exemplo, para converter 33 da base 10 para a base 2,
será exibida a seguinte explicação: 33 ÷ 2 = 16 with a remainder of 1 16 ÷ 2 = 8 with a remainder of 0 8 ÷ 2 = 4 with a remainder of 0 4 ÷ 2 = 2 with a remainder of 0 2 ÷ 2 = 1 with a remainder of 0 1 ÷ 2 = 0 with a remainder of 1 Now collect the remainders from the bottom up and put
them together to form the base 2 number. The number is 100001 Essa explicação pode ser traduzida da seguinte maneira: 33 ÷ 2 = 16
com um resto de 1 16 ÷ 2 = 8 com
um resto de 0 8 ÷ 2 = 4
com um resto de 0 4 ÷ 2 = 2
com um resto de 0 2 ÷ 2 = 1
com um resto de 0 1 ÷ 2 = 0
com um resto de 1 Agora pegue
os restos de baixo para cima coloque-os juntos para formar o número na base 2. O número é 100001. Você pode
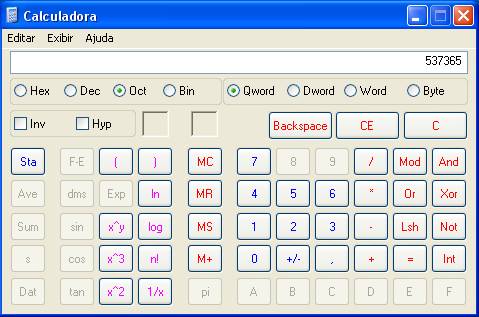
conferir sua conversão usando, também, a Calculadora do sistema operacional
Microsoft Windows. Entre Ao escolher
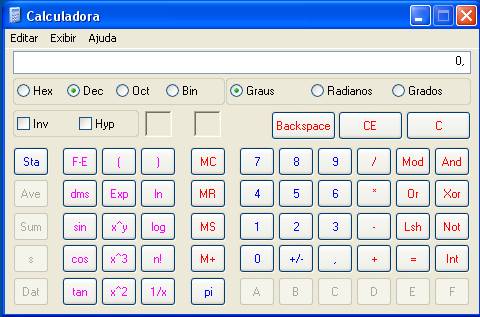
Exibir->Cientifica, a Calculadora passará a ter a seguinte aparência: Se você
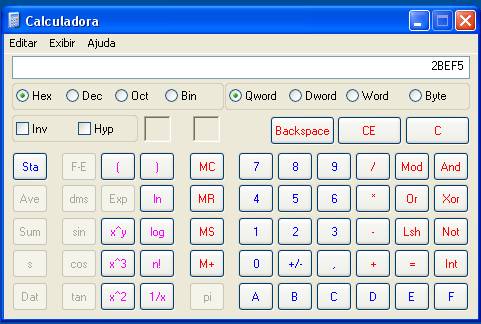
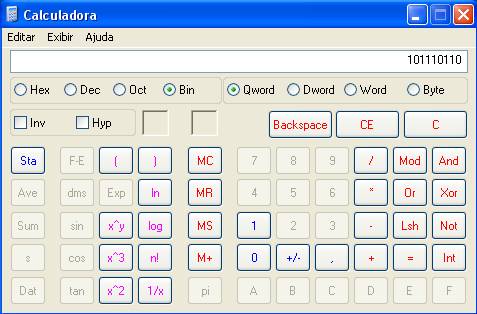
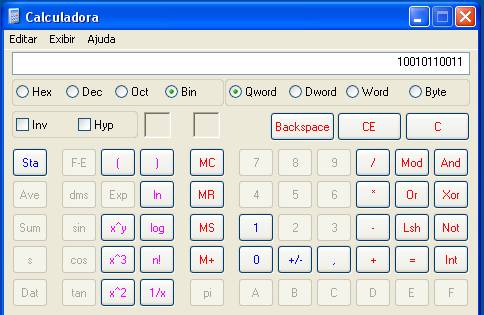
quiser converter (2BEF5)16 para base octal
( ) 8 , por exemplo, basta
clicar no botão Hex, digitar 2BEF5 e depois clicar em
Oct , como no exemplo abaixo: Adição binária Tente fazer
os seguintes exercícios de adição PLT - Página 60 – 14) e) (1100111101)2 + (101110110)2 Para
conferir, faça a soma usando a Calculadora do Windows, usando as sugestões
apresentadas acima. Exercício 4) da última lista. Seja S o
resultado da soma dos números binários X e Y, onde: X= 00110010 Y= 01010111
Qual o valor de S em hexadecimal (CAPES
Analista de Sistemas - 2008 - banca CESGRANRIO)? a) BA b) A5 c) 59 d) 89 e) 137 Confira o último
exercício usando http://faculty.mc3.edu/ Você pode
conferir, também, usando a Calculadora do Windows (embora o link acima aponte
para um recurso mais instrutivo e didático, a saber, um applet –
uma aplicação escrita na linguagem de programação Java, que executa na sua máquina,
usando o seu navegador/browser, como o Internet Explorer ou Firefox) Consulte o
material que trata de Tabelas
Verdade Verifique,
depois, o material que trata de Álgebra
Booleana e Portas Lógicas Nesse
último material, procure ler de forma mais detalhada a parte referente a Portas
Lógicas. Nas
próximas atividades (baseadas no material disponível em http://www.cs.gordon.edu/courses/cs111/paperwork/labs/Circuits%20Lab_2008.pdf)
você estará usando o simulador disponível em http://www.manuf.bme.hu/gdf/LogicSim/LogicSim.htm Esse simulador também está disponível em http://www.lnaffah.com/ioc/LogicSim/LogicSim.htm Atividade 1 Construa um
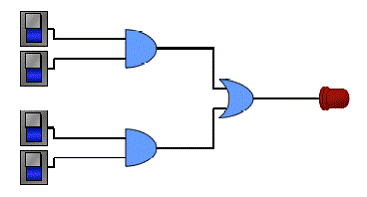
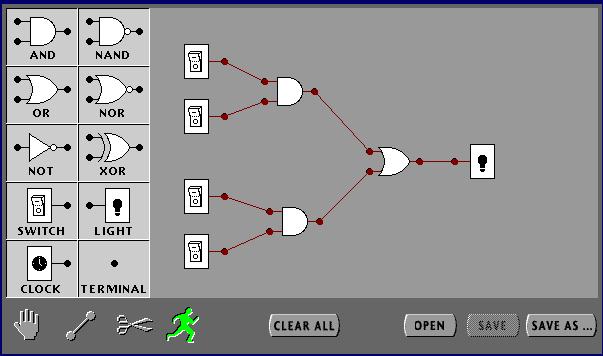
circuito como abaixo: Os demais
desenhos referem-se às portas lógicas (AND, NAND, OR, NOR, NOT, XOR) Clear all – limpa toda a área de trabalho Open – abre
um diagrama/circuito salvo Save –
salva um diagrama/circuito Save as –
salva num novo local ou com um novo nome Construa
uma tabela verdade correspondente a esse circuito, com todas as combinações
possíveis para interruptor ligado e desligado Entrada A Entrada B Entrada C Entrada D
Saída Atividade 2 1.
Desenhe
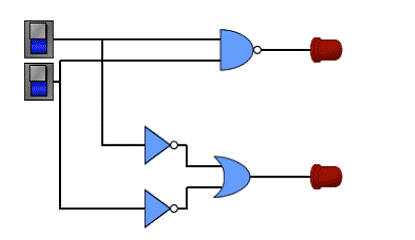
um circuito com dois interruptores. 2.
Desenhe
uma porta NAND e uma porta OR, cada uma com sua própria saída luminosa. 3.
Desenhe
duas portas NOT (portas inversoras) ligadas nas entradas da porta OR 4.
Ligue
as entradas da porta NAND e das portas NOT (inversoras) aos interruptores. 5.
O
diagrama deverá ter um aspecto similar ao abaixo: 6.
Coloque
o circuito para funcionar e tente todas as combinações possíveis de ligado e
desligado. Liste os resultados na tabela verdade abaixo. O que você
observou? A B Saída 1 Saída 2 Aula
Prática 2 Atividade 3 Crie uma
expressão booleana e um circuito a partir de uma tabela verdade. 3.1) Use
o algoritmo da soma de produtos para converter a tabela verdade abaixo numa
expressão booleana A B C Resultado
0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1 Expressão
booleana 3.2) Coloque
o circuito correspondente na área de trabalho, verifique se ele funciona
corretamente e salve-o.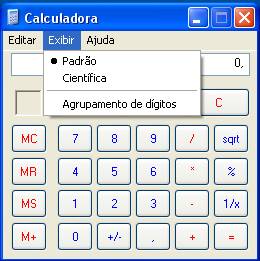
Modo de construção (para arrastar os objetos
do lado esquerdo a área de trabalho do lado direito)
Modo de ligação (para ligar os objetos e
construir o circuito/diagrama)
Modo de recorte (para remover itens do circuito/diagrama
construído)
Modo de execução (para colocar o
circuito/diagrama em funcionamento)
Interruptor (chave liga e desliga – pode ser
ligada/desligada no modo de execução)
Lâmpada (exibe ou não luz no modo de execução,
denotando a passagem ou não de corrente, isto é, saída 1 ou 0)
Relógio (alterna entre um sinal ligado e
desligado periodicamente, isto é, em intervalos regulares)
Terminal (faz a conexão entre dois pontos)
