ÁLGEBRA BOOLEANA
Foi um modelo formulado por George Boole, por volta de 1850.
Observando a lógica proposicional e a teoria de conjuntos verificamos que elas possuem propriedades em comum.
Lógica Proposicional
|
1a. A Ú B = B Ú A |
1b. A Ù B = B Ù A |
(propriedades comutativas) |
|
2a. (A Ú B) Ú C = A Ú (B Ú C) |
2b. (A Ù B) Ù C = A Ù (B Ù C) |
(propriedades associativas) |
|
3a. A Ú (B Ù C) = (A Ú B) Ù (A Ú C) |
3b. A Ù (B Ú C) = (A Ù B) Ú (A Ù C) |
(propriedades distributivas) |
|
4a. A Ú F = A |
4b. A Ù V = A |
(propriedades de identidade) |
|
5a. A Ú Ø A = V |
5b. A Ù Ø A = F |
(propriedades de complemento) |
Teoria de Conjuntos
|
1a. A È B = B È A |
1b. A Ç B = B Ç A |
(propriedades comutativas) |
|
2a. (A È B) È C = A È (B È C) |
2b. (A Ç B) Ç C = A Ç (B Ç C) |
(propriedades associativas) |
|
3a. A È (B Ç C) = (A È B) Ç (A È C) |
3b. A Ç (B È C) = (A Ç B) È (A Ç C) |
(propriedades distributivas) |
|
4a. A È Æ = A |
4b. A Ç S = A |
(propriedades de identidade) |
|
5a. A È A’ = S |
5b. A Ç A’ = Æ |
(propriedades de complemento) |
Definição:
Uma álgebra booleana é um conjunto B no qual são definidos duas operações binárias ( + e . ) e uma operação unária ( ’ ) e no qual existem dois elementos distintos 0 e 1 tais que valem as seguintes propriedades para todo A, B e C pertencentes a B:
|
1a) A + B = B + C |
1b) A . B = B . C |
(propriedades comutativas) |
|
2a) (A + B) + C = A + (B + C) |
2b) (A . B) . C = A . (B . C) |
(propriedades associativas) |
|
3a) A + (B . C) = (A + B) . (A + C) |
3b) A . (B + C) = (A . B) + (A . C) |
(propriedades distributivas) |
|
4a) A + 0 = A |
4b) A. 1 = A |
(propriedades de identidade) |
|
5a) A + A’ = 1 |
5b) A . A’ = 0 |
(propriedades de complemento) |
Denotamos uma álgebra booleana por [B, +, ×, ’, 0, 1].
Exemplo: Seja B = {0, 1} e as operações + e . definidas em B como A + B = max(A, B) e x × y = min(A, B). E seja ’ definida pela tabela:
|
A |
A’ |
|
0 |
1 |
|
1 |
0 |
Para verificarmos se as propriedades são válidas, basta testarmos todas as possibilidades possíveis para cada uma.
Teorema da Unicidade do Complemento
Para qualquer x na álgebra booleana, se existir um x1 tal que A + A1 = 1 e A . A1 = 0, então A1 = A’.
Existem outras propriedades que valem para qualquer álgebra booleana:
|
6a) A + A = A |
6b) A . A = A |
(propriedades idempotentes) |
|
7a) A + 1 = 1 |
7b) A . 0 = 0 |
(propriedades de identidade) |
|
8a) A + (A . B) = A |
8b) A . (A + B) = B |
(propriedades de absorção) |
|
9a) (A + B)’ = A’ . B’ |
9b) (A . B)’ = A’ + B’ |
(leis de De’Morgan) |
|
10a) 0’ = 1 |
10b) 1’= 0 |
(propriedades de complemento) |
|
11) (A’)’ = A |
|
|
Exercício
Prove que:
a) A . [B + (A . C)] = (A . B) + (A . C)
b) (A + B) . (A’ + B) = B
c) (A + B) + (B . A’) = A + B
Expressões Booleanas
Uma expressão booleana com n variáveis, x1, x2, ..., xn, é uma cadeia finita de símbolos formados pela aplicação das seguintes regras:
1. x1, x2, ..., xn são expressões booleanas.
2. Se P e Q são expressões boolenas, então (P + Q), (P . Q) e (P’) também são.
Exemplos de expressões booleanas
(((A + B) ’) . C )
((A’ + (B . C)’) + D)
Função-Verdade
Uma função-verdade é uma função f tal que f:{0, 1}n ® {0, 1} para algum inteiro n ³ 1.
A tabela-verdade para a operação booleana + descreve uma função-verdade f com n = 2.
f(0, 0) = 0, f(0, 1) = 1, f(1, 0) = 1, f(1, 1) = 1.
A tabela-verdade para a operação booleana . descreve outra função-verdade para n = 2.
f(0, 0) = 0, f(0, 1) = 0, f(1, 0) = 0, f(1, 1) = 1
O operador booleano ’ descreve outra função para n = 1.
f(0) = 1, f(1) = 0
Qualquer expressão booleana define uma única função-verdade.
Exemplo:
A expressão booleana (A + B’) . (A + C), define uma função-verdade f tal que f:{0,1}3 ® {0,1}.
f(0, 0, 0) = 0
f(0, 0, 1) = 1
f(0, 1, 0) = 0
f(0, 1, 1) = 0
f(1, 0, 0) = 1
f(1, 0, 1) = 1
f(1, 1, 0) = 1
f(1, 1, 1) = 1
Redes Lógicas
Imagine que as voltagens transmitidas entre os fios possam assumir dois valores, um alto e o outro baixo, representados por 1 e 0.
Suponha ainda que existem dispositivos básicos denominados portas ou (or), porta e (and) e inversor ( ou porta não, ou porta not), que se comportam como o “ou”, o “e” e o “ ’ ” da lógica proposicional.
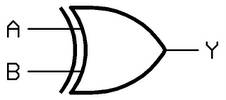
Essas portas são representadas pelos símbolos:
Porta OR Porta AND Inversor
Redes e expressões
Combinando portas AND, OR e inversores, podemos construir uma rede lógica que represente uma expressão booleana.
A rede lógica para a expressão booleana (A + B’) . (A + B) é:
Exercícios
1. Projete uma rede lógica para cada expressão booleana a seguir:
a) A’ . B
b) ( A + B) . (B + C)’
c) ((A + B’) . (B + C’) )’
2. Escreva uma expressão booleana para:
Outras portas lógicas
![]()
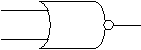
Porta NOR Porta NAND
Porta XOR
Forma Canônica
Objetivo: Encontrar uma expressão booleana que corresponda a uma função-verdade arbitrária.
Expressões booleanas tais como x ou y’ consistindo de simples variáveis ou de seu complemento são denominadas literais.
Um mintermo em n varáveis é o produto de n literais, onde cada literal envolve uma variável diferente.
Um mintermo é uma expressão booleana que só retorna 1 para uma única combinação de 0’s e 1’s.
As expressões AB’C e A’B C’são mintermos com três variáveis A, B e C.
Sendo que AB’C só retorna 1 se x = 1, y = 0 e z =1.
A expressão AC em não é um mintermo em três variáveis A, B e C, mas é um mintermo em duas variáveis x e z.
A expressão ABA’C não é um mintermo em três variáveis A, B, C.
A tabela a seguir lista os 8 elementos de {0, 1}3 e os correspondentes mintermos que tomam o valor 1 para o elemento indicado.
|
A B C |
|
|
(0, 0, 0) |
A’B’C’ |
|
(0, 0, 1) |
A’B’C |
|
(0, 1, 0) |
A’BC’ |
|
(0, 1, 1) |
A’BC |
|
(1, 0, 0) |
AB’C’ |
|
(1, 0, 1) |
AB’C |
|
(1, 1, 0) |
ABC’ |
|
(1, 1, 1) |
ABC |
Para encontrarmos uma expressão para uma determinada função-verdade basta somarmos os mintermos obtidos para cada situação onde a função retorne valor 1.
Exemplo: Seja a função-verdade f como f:{0,1}3 ® {0,1}, definida pela tabela.
|
A B C |
f(A, B, C) |
|
0 0 0 |
0 |
|
0 0 1 |
0 |
|
0 1 0 |
1 |
|
0 1 1 |
0 |
|
1 0 0 |
1 |
|
1 0 1 |
1 |
|
1 1 0 |
1 |
|
1 1 1 |
0 |
Uma expressão booleana correspondente seria A’BC’ + AB’C’ + AB’C + ABC’.
Esta expressão booleana, correspondente à função-verdade, e formada pela soma de mintermos é denominada forma canônica de mintermos ou forma normal disjuntiva.
Exercício:
Encontre a forma canônica de mintermos de:
a. AB + A’B’ com 3 variáveis A, B e C.
b. x.(A + B’) com 3 variáveis A, B, C.
c.
|
A B C |
f(A, B, C) |
|
0 0 0 |
0 |
|
0 0 1 |
1 |
|
0 1 0 |
1 |
|
0 1 1 |
0 |
|
1 0 0 |
0 |
|
1 0 1 |
1 |
|
1 1 0 |
0 |
|
1 1 1 |
1 |
Minimização
Circuitos lógicos representam expressões booleanas. Portanto, é interessante simplificar expressões booleana para obtermos circuitos simplificados.
Vamos utilizar um procedimento que permite obter uma soma de produtos mínima.
Esta soma de produtos, não necessariamente, é a expressão mais simples.
Exemplo: Seja a expressão
ABC + A’BC + A’BC’
Uma soma de produtos mínima equivalente seria
BC + A’B
No entanto, esta expressão é equivalente a B(C + A’) que requer um número menor de portas lógicas na construção de sua rede lógica.
Exercício:
Simplifique as expressões booleanas a seguir para que elas tenham o número indicado de literais.
a. A’B’ + AB + A’B - dois literais
b. (A + B)(A + B’) - 1 literal
c. A’B + AB’ + AB + A’B’ - 1 literal